- Författare Matthew Elmers [email protected].
- Public 2023-12-16 22:35.
- Senast ändrad 2025-01-24 09:36.

Vad avgör noggrannhet - en av de viktigaste egenskaperna hos ett vapen? Uppenbarligen från kvaliteten på fatet och patronen. Låt oss skjuta upp patronen för nu, men överväga processens fysik.
Ta en metallstav eller -rör av elastisk metall och fixera det hårt i en massiv bas. Så vi får en modell av enheten som studeras. Nu, om vi träffar stången, spelar det ingen roll på vilken plats och i vilken riktning, antingen dra tillbaka den eller klämma den eller, till sist, sätta in en patron i röret och skjuta ett skott, vi kommer att se att stången (fat) har kommit in i en dämpad oscillerande rörelse. Dessa vibrationer sönderdelas till det enklaste, och varje typ av en så enkel vibration av pipan kommer att påverka skottets noggrannhet (noggrannhet) på sitt eget sätt.
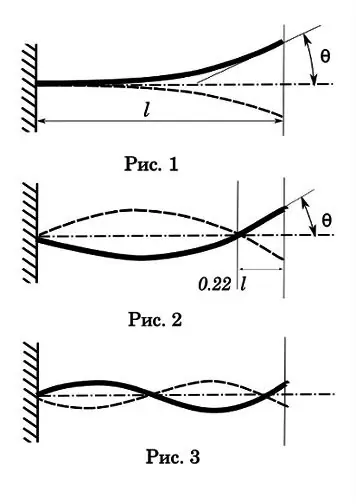
Låt oss börja med första ordningen eller tonvibrationer. Som du kan se (fig. 1) har en sådan svängning endast en nod vid fästpunkten, den största amplituden, den längsta sönderfallstiden och den längsta oscillationstiden för en period. Den här tiden är 0,017-0,033 sek. Kulets restid genom hålet är 0, 001-0, 002 sek. Det vill säga betydligt mindre än cykeln för en oscillation, vilket innebär att denna typ av oscillation inte har någon signifikant effekt på noggrannheten hos ett enda skott. Men med automatisk fotografering kan en intressant bild visa sig. Låt oss säga att eldhastigheten är 1200 rds / min, d.v.s. tid för en cykel - 0,05 sek. Med en första ordnings oscillationsperiod på 0, 025 sek har vi ett multipelfrekvensförhållande. Och detta är en oumbärlig förutsättning för resonans med alla följder som följer - vapnet börjar skaka med sådan kraft att det kan falla sönder.
Låt oss gå vidare till svängningar av andra ordningen (bild 2). Men jag föreslår att humaniststudenter först genomför ett experiment för att eliminera bristerna i utbildning inom fysik. Du måste ta en liten pojke (du kan en tjej), sätta honom på en gunga och gunga. Innan du är en pendel. Stå vid sidan av gungan och försök att slå pojken med bollen. Efter en rad försök kommer du fram till att det bästa sättet att träffa är när målet är i den första oscillationsfasen - den maximala avvikelsen från jämviktspunkten. Vid denna tidpunkt har målet noll hastighet.
Låt oss titta på diagrammet av andra ordningen. Den andra vibrationsnoden är belägen cirka 0,22 från pipens ände. Denna punkt är en naturlag, det är omöjligt att skapa sådana vibrationer för fribäraren så att den andra noden faller på den fria änden. Det är där det är och beror inte på pipans längd.
Oscillationsamplituden för andra ordningens schema är lägre, men oscillationstiden är redan jämförbar med tiden för kulan genom borrningen-0, 0025-0, 005 sek. Så för singelfotografering är detta redan av intresse. För att göra det klart vad vi pratar om, föreställ dig ett fat som är 1 meter långt. Kulan färdas genom hela pipan på 0, 001 sekunder. Om oscillationsperioden är 0,004 sek, då når kulan lämnar pipan, når tunnan sin maximala böjning i den första fasen. Frågan för humaniora är - vid vilken tidpunkt (i vilken fas) är det bäst att skjuta en kula ur fatet för att säkerställa konsekvens i resultaten? Kom ihåg gungan. Vid nollpunkten är vektorn för stamavböjningshastigheten maximal. Det är svårare för en kula att träffa denna punkt på fatskärningen, den har också sitt eget fel i hastighet. Det vill säga det bästa ögonblicket för kulan att flyga ut blir när pipan är på den högsta punkten i den första avböjningsfasen - som i figuren. Då kommer obetydliga avvikelser i kulhastigheten att kompenseras av den längre tid som tunnan spenderar i sin mest stabila fas.
En grafisk framställning av detta fenomen kan tydligt ses i diagrammet (bild 4-5). Här - Δt är tidsfelet med vilket kulan korsar pipans nosparti. I fig. 4 är idealisk när den genomsnittliga starttiden för kulor sammanfaller med nollfasen i piposcillationen. (Matematiker! Jag vet att hastighetsfördelningen är olinjär.) Det skuggade området är banornas spridningsvinkel.
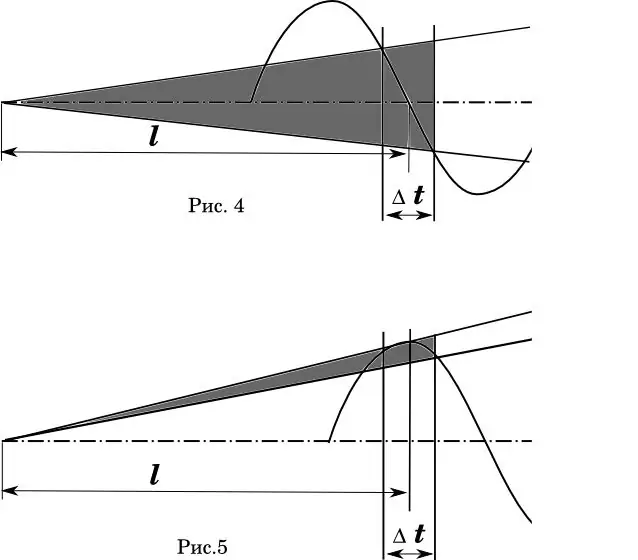
I fig. 5 förblir cylinderns längd och hastighetsfel desamma. Men fasen för fatböjningen förskjuts så att den genomsnittliga avgångstiden sammanfaller med den maximala avböjningen av pipan. Är kommentarer överflödiga?
Är det värt ljuset? Hur allvarliga kan avvikelserna som orsakas av andra ordningens svängningar vara? Allvarligt och mycket allvarligt. Enligt sovjetprofessorn Dmitry Aleksandrovich Ventzel erhölls följande resultat i ett av experimenten: radien för medianavvikelsen ökade med 40% med en förändring i fatlängden med bara 100 mm. För jämförelse kan en högkvalitativ fatbearbetning förbättra noggrannheten med bara 20%!
Låt oss nu ta en titt på formeln för vibrationsfrekvensen:
var:
k - koefficient för andra ordningens svängningar - 4, 7;
L är pipans längd;
E är elasticitetsmodulen;
Jag är sektionens tröghetsmoment;
m är stammens massa.
… och fortsätt till analysen och slutsatserna.
Den uppenbara slutsatsen från figurerna 4-5 är felhastighetsfel. Det beror på pulverets kvalitet och dess vikt och densitet i patronen. Om detta fel är minst en fjärdedel av cykeltiden kan allt annat avstå. Lyckligtvis har vetenskap och industri uppnått mycket stor stabilitet i denna fråga. Och för de mer sofistikerade (i till exempel bänkstöd) finns alla förutsättningar för självmontering av patroner för att justera kulans släppfas exakt till fatlängden.
Så vi har en patron med lägsta möjliga hastighetsvariation. Fatlängden beräknades utifrån dess maximala vikt. Frågan om stabilitet uppstår. Vi tittar på formeln. Vilka variabler påverkar förändringen i oscillationsfrekvensen? Fatlängd, elasticitetsmodul och massa. Tunnan värms upp under avfyrning. Kan värme ändra fatlängd så att noggrannheten påverkas. Ja och nej. Ja, eftersom denna siffra ligger inom hundradelar av en procent för en temperatur på 200 C. Nej, eftersom förändringen i stålets elastiska modul för samma temperatur är cirka 8-9%, för 600C är det nästan två gånger. Det vill säga många gånger högre! Tunnan blir mjukare, pipens böjningsfas förskjuts framåt i det ögonblick som kulan lämnar, noggrannheten sjunker. Tja, vad säger en tankeväckande analytiker? Han kommer att säga att det är omöjligt att få maximal noggrannhet på en fatlängd i kallt och varmt läge! Vapnet kan ha en bättre prestanda med antingen ett kallt eller varmt fat. Följaktligen erhålls två klasser av vapen. Den ena är för bakhållsåtgärder, när målet måste träffas från det första - "kalla" skottet, eftersom noggrannheten i det andra kommer att bli sämre på grund av den oundvikliga uppvärmningen av pipan. I ett sådant vapen finns det inget brådskande behov av automatisering. Och den andra klassen är automatgevär, vars fatlängd är anpassad till det heta fatet. I detta fall kan en eventuell miss på grund av den låga noggrannheten för ett kallskott kompenseras av ett snabbt efterföljande varmt och mer exakt skott.
EF Dragunov kände mycket väl till den här processens fysik när han designade sitt gevär. Jag föreslår att du bekantar dig med historien om hans son Alexei. Men först måste någon bryta deras hjärnor. Som ni vet närmade sig två prover av Konstantinov och Dragunov finalen i tävlingen om ett prickskyttegevär. Formgivarna var vänner och hjälpte varandra i allt. Så Konstantinovs gevär "stämde" till kallt läge, Dragunovs gevär till "hett". För att förbättra noggrannheten i rivalens gevär skjuter Dragunov sitt gevär med långa pauser.

Låt oss titta på formeln igen. Som du kan se beror frekvensen också på fatets massa. Stamens massa är konstant. Men hård kontakt med framdelen ger en oförutsägbar positiv feedback till fatet. Systemet-fat-forend-arm (stöd) kommer att ha ett annat tröghetsmoment (en uppsättning massor relativt fästpunkten), vilket innebär att detta också kan orsaka ett fasskifte. Det är därför idrottare använder mjukt stöd. Samma särdrag är förknippat med tillämpningen av principen om "hängande fat", när vapnets framkant inte har en hård kontakt med pipan och är fast fastsatt på den (vapnet) endast i området av vapnet mottagaren, och den andra änden rör antingen inte alls eller rör genom en fjäderbelastad led (SVD).
Sista tanken. Det faktum att det med samma fatlängd är omöjligt att uppnå samma noggrannhet vid olika temperaturer ger en utmärkt anledning att sträcka ut hjärnan. Det är bara nödvändigt att ändra pipans längd och / eller massa när pipans temperatur ändras. Utan att ändra varken pipans längd eller vikt. Ur humaniora är detta en paradox. Ur teknisk synvinkel, en idealisk uppgift. Hela livet för en designer är kopplad till lösningen av sådana problem. Sherlocksna vilar.






